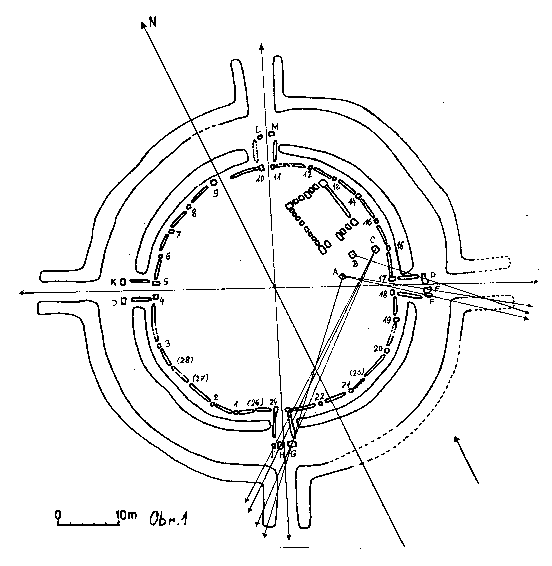
Rondel in Buč
any possibly served as a solar and lunar observatory.Vladimir Karlovský, Observatory and Planetarium Hlohovec
, vladokarlovsky@hotmail.comTranslation: Patricia Lipovská,
Abstract
A preliminary analysis of the Bučany rondel's astronomical orientation was made in the paper. With archeologically determined age of -3800 +/-150 years the author has found th
at 9 of the Rondel's 12 extreme directions have significant astronomical orientation. The analysis shows that it could have been used for observations of the Sun at summer and winter solstices, so called low Moon at winter and summer solstices, and so called high Moon at summer and winter solstices. The possibility of use of the low Moon descent at the summer solstices to time spring agricultural works and taking crops, and also a possible division of a year into three calendar periods has been shown.1. Introduction
Firstly, the archeological content of the term "rondel" should be described. In Neolithic it was a space enclosed in a regular circle by up to 4 metres deep pointed ditch. The ditch is regularly broken at the cardinal points (there are some certain deflections off the due directions) so that natural bridges about 2 metres wide - entrances into the interior area form. One or two rings of wooden palisades follow the ditch in the interior area. These are broken at the entrances leading into the interior so that they form entrance corridors. Rondels are usually small with the diameter of 40 - 70 metres, middle with the diameter of 80 -120m, but also big with 140 - 300m. Podborský 1983.
The peasants' settlement in Bučany according to the acquired arche
ological material falls into the neolith (4,000 BC). This period in the region of Western Slovakia is characterized by findings of ceramics with engraved and painted ornamentation mostly of red and rarely also yellow and white colour, which is archeologically classified with the early stage of lengyel culture called after the locality of Lengyel, Hungary. Bujna J., Romsauer P. 1987. Details can be also found in papers of Bujna J., Rosmauer P. 1986 where dimensions of the ditches, palisades and interior objects of rondels can be also found.2. Main Dimensions.
The diameter of the interior palisade of the Rondel is 45.5m. It forms a regular circle with the deviation of 5.9 per cents. The ditches are also shaped in regular circles with the inner ditch deviation of 8.4 per cents and the outer one of 7.9 per cents from a regular circle. Both the palisade and ditches are broken in 4 points that represent the cardinal points and form entrances into the interior. A building that ressembles a megaron is situated in the interior. Figure 1 provides a better picture of dimensions and objects of the interior. As it is not possible to measure the Rondel accurately in the terrain the depicted directions and their respective azimuths were determinated with accuracy of 0.2 degree. The main directions that are present in the object were assigned according to its plan. See also : Bujna J.,Romsauer P.,1982.If the plan was oriented towards the magnetic north pole, which is very probable, it is necessary to make corrections of the d
irections considering the magnetic declination (while making the measurements in Bučany it was +26min (0.433deg.) See :Bucha V.,1975,p.26-49 Astronomical azimuths are considered, which are directions described in the section 3.2.

Fig. 1. Plan of the Rondel in Bučany by Bujna J., Romsauer P., 1986. Depicted are astronomically significant directions.
3. Astronomically assigned directions.
In oder to check for coincidences in the orientation of the Rondel i
n Bučany with ascends and descends of the Sun and Moon below the real horizon it is necessary to transform the equatorial coordinates into the horizontal ones. In this case the aim is to determine the astronomical azimuths of ascend and descend points of celestial bodies, which increases from due south counter clockwise (towards west). It differs from the azimuth used in army, which starts at due north. There is an equation for the astronomical azimuth A = Av - 180deg where A is the astronomical azimuth and Av is the azimuth.
In general the azimuths of ascend or descend points can be computed as follows:
cos A = - ( sin
d - sin f sin h) / ( cos f cos h ) [ 1 ]
If the azimuth used in army is in question the following equation can be used:
cos A V = ( sin
d - sin f sin h ) / ( cos f cos h ) [ 2 ]
where
d is declination of he body, f latitude of the observation site, h is height of the visible horizon. See : Chalchunov V.Z.,1972 and Wood E.J.,1978 , Wood E.J.1981. If azimuth of ascent and descent points at the real horizon has to be determined the fact that location of the Sun and Moon, e.i. their equatorial coordinates are related to the Earth´s centre ( they are geocentric) has to be considered. This is why the transformed coordinates have to be corrected to make them topocentric. Height of the visible horizon has to be corrected to consider the refraction, horizontal equatorial parallax, curvature of the Earth and whether the touch of the disk with the horizon, or centre of the disk, or the point where the disk disappears below the horizon is the case as the Sun´s and the Moon´s angular dimensions are not equal to zero. If h0 is astronomical height of the horizon then:h0 = arc tg (( H - H0 ) / d ) [ 3 ]
where H0 is altitude of the observation site, H represents altitude of a distant horizon and d is distance of the horizon in metres.
Refraction values can be found in refraction tables published for example in the following:Hawkins G.S.,1977and Berliner Astronomisches Jahrbuch 1959, Astronomičeskij Ježegodnik 1979. The best refraction table can be found in the Astronomičeskij kalendar ,postajannaja časť 1981 where the refraction values at 10
o C and atmospheric pressure of 1013hPa up to the zenith distance of 90deg, e.i. 0 deg height from 80 deg (10deg of height) in step of 10 angular minutes are given. Considering the influences of temperature and pressure the refraction values can be corrected as follows:r = r0 ( 1 - 0,036 ( T - T0 ).0,0010 ( P - P0 )). exp ( - H / 8400 ) [4]
where T0 = 10o C , P0 = 1013 hPa (normal pressure), r0 is mean atmospheric refraction in a height h0
The normal pressure value of 1002hPa (1002 mbar) given by Hawkins G.S.,1977 is incorrect , H is the altitude.
To make a topocentric correction of the height it is necessary to consider the horizontal equatorial parallax of the body. For Sun the parallax is from 8.649" (0.0024025deg) to 8.944" (0.00248444deg). The mean value is 8.794097" (0.0024428deg). With the Moon the parallax varies from 53´54.6" (0.8985 deg )to 61´31.4" (1.025388 deg). Mean value is 57´2.6" (0.950722 deg)
If the horizon is very distant a curvature of the Earth must be considered. The correction value is incorrectly given by Wood E.J.,1981 p.87 and also by Weber Z.,1985 to be 0.0045deg per 1 km of the distance. The correct value is 0.004496605 deg per 1km of distance as given by Duncan J.Ch.,1946,p.82-83.
Angular dimensions of a body must be also considered as there are differences in azimuth values of touching body with the horizon, of the centre of the body and of a disappearing body below the horizon. As other authors believe Hawkons G.S.,1977, it seems that touches of the Sun and Moon with the horizon were observed in the Rondel as these are simplest to observe and are relatively occurate. Angular dimensions - diameters of the Sun vary from 31´31.34" in aphelion to 32´35.78" in perihelion. The mean is 31´59.26" (0.5331277 deg). Angular dimensions - diameters of the Moon vary from 29´20" in apogee to 33´ 32" in perigee. The mean value is 31´5.16" (0.5181 deg)
3.1 Correction to the height.
To correct the height the following equation is used:
h = h0 - r + p - k + q [5 ]
where h0 is astronomical height of a horizon given by equation [3], r is refraction computed in the equation [4], where r0 is tabulated in the refraction table, p is a horizontal equatorial parallax of a body, k is the correction due to the curvature of Earth, q is the angular radius of the body. Equation [5] is valid for the touch of the body with the horizon. For disappeared body q<0 and for the centre of the body q=0.
Equation [5] can be applied on the Sun as follows:
h = h0 - r + 0,0024428 - k + 0,2665638 [ 6 ]
on the Moon:
h = h0 - r + 0,950722 - k + 0,25605 [ 7 ]
In both cases mean diameter and parallax values were used.
k=(0.004496605) . ( the distance of the real horizon in kms.)
Mean refraction values in relation to h0.
|
h0 |
r0 |
r0 in degs |
|
0o 00' |
35' 24" |
0.589999 |
|
0o 10' |
33' 11" |
0.553055 |
|
0o 20' |
31' 09" |
0.519167 |
|
0o 30' |
29' 18" |
0.488333 |
|
0o 40' |
27' 36" |
0.460000 |
|
0o 50' |
26' 03" |
0.434167 |
|
1o 00' |
24' 37" |
0.410278 |
|
1o 10' |
23' 19" |
0.388611 |
|
1o 20' |
22' 07" |
0.368611 |
|
1o 30' |
21' 01" |
0.350278 |
|
1o 40' |
20' 02" |
0.333889 |
|
1o 50' |
19' 08" |
0.318889 |
|
2o 00' |
18' 18" |
0.305000 |
|
2o 10' |
17' 32" |
0.292222 |
|
2o 20' |
16' 49" |
0.280278 |
|
2o 30' |
16' 09" |
0.269167 |
|
2o 40' |
15' 31" |
0.258611 |
|
2o 50' |
14' 55" |
0.248611 |
|
3o 00' |
14' 22" |
0.239444 |
3.2 Main data of the Rondel in Bučany
The geographical coordinates of the Rondel are:
latitude 48o 25,5' = 48.425 degs
longitude 17o 41' = 17.683333 degs east
altitude H0 = 160 m
Date: 3800 +/- 150 B.C.
Directions and distances towards the relevant real horizon:
|
Direction |
Azimuth (degs) |
Altitude (m) |
Distance (m) |
|
Western entrance |
115.5 |
768 |
25 400 |
|
Eastern entrance |
295.5 |
200 |
8 900 |
|
A - E |
306 |
230.6 |
9 500 |
|
A - F |
309 |
230.6 |
9 500 |
|
E - A |
126 |
480 |
26 000 |
|
F - A |
129 |
480 |
26 000 |
|
C - I |
54 |
160 |
8 600 |
|
C - H |
52.5 |
160 |
8 600 |
|
C - G |
50 |
160 |
8 600 |
|
G - C |
230 |
240 |
11 000 |
|
H - C |
232.5 |
240 |
11 000 |
|
A - G |
43.5 |
160 |
8 600 |
|
G - A |
223.5 |
280 |
14 400 |
|
B - D |
44 |
230 |
9 500 |
Visibility of all the horizons is good because the site is elevated 12 - 15m above the surrounding terrain and possible bushes would not affect the view.
3.3 Computation of azimuth.
Equation [1] is used to compute the azimuth. In Rondel in Bučany, ho
wever, azimuths of extreme declinations of the Sun and Moon are the issue. With Sun the extreme declinations occur at summer and winter solstices and they are equal to the inclination of the ecliptic towards the celestial equator, with positive and negative signs respectively e.i. the declination at the summer solstice is + e and it is - e at the winter solstice. Using equation [1] obtained are two azimuths for summer solstice (at sunrise and sunset) and two azimuths for winter solstice (at sunrise and sunset). The inclination of the ecliptic changes with time, however, and its value is computed for the past as follows:e
= 23,452294 - 0,0130125 TS - 1,63888.10-6 (TS)2 + 5,02777.10-7 (TS)3 + De + de [ 8]where inclination of the ecliptic is in degrees, TS is time, which has passed since 1900.0 in tropical centuries given by 36524.22 days;
De is long periodical part and de is short periodical part of ecliptic inclination nutation. See:Astronomičeskij ježegodnik 1979a
With the Moon the extreme values differ from those of the Sun because the path of the Moon is inclined to the ecliptic. i = 5o 8' 43.4" (changes with period of 173 days from 4o 59' to 5o 19' ). Inclination of the path of the Moon to the ecliptic is 5,14539 +/- 0.167 degs. Extreme declination of the Moon values therefore are (
e + i ) and ( e - i ). The values vary from the maximum (high Moon) to the minimum (low Moon) with period of 9.305 years. It reaches the maximum every 18.61 years. With the Moon therefore extreme declination values at the summer solstice ( e + i ) and ( e - i ) and at the winter solstice -( e + i ) and -( e - i ) exist. In total 8 azimuths, 4 at the ascend and 4 at the descend of the Moon exist.
3.3.1 Computations.
To compute azimuths first it is necessary to determine height values h0 . These are for the following directions as follows:
|
direction |
h 0 ( in degrees) |
|
Western entrance |
1,371 |
|
Eastern entrance |
0,258 |
|
A - E , A - F |
0,426 |
|
C - I , C - H |
0 |
|
|
|
Inclination of the ecliptic in -3800 ( TS = - 57 ) is:
e
= 24,095571Example:
For the western entrance the following can be written (descent of the low Moon, touch of the disk with horizon):
h = 1,371 - 0,364 + 0,951 - 0,117 + 0,256
h = 2,097 deg
e
= 24,095571d
= e - i = 18,950181 degr is being computed at + 15oC as there was a warmer climate compare to the present one.
To compute azimuth at the descend the equation [1] is used:
A = 116,780 deg
In this way all other azimuths can be computed.
Then they can be compared with those found in the Rondel.
Follows the comparison of the astronomical orientation found in the Rondel with that computed. All data are in degrees: the computation was made for touches of the Sun and Moon with horizon.
|
Direction |
Horsky Z.,1986l corrected with magnetic declination |
Rondel |
Result of computation |
Difference result minus Rondel |
Difference result minus Horsky 1986 |
Astron. direction |
|
Western entrance |
114,43 |
115,5 |
116,78 |
1,28 |
2,35 |
+ ( e - i ) the Moon |
|
Eastern entrance |
|
295,5 |
297,99 |
2,49 |
|
- ( e - i ) the Moon |
|
A - G |
42,73 |
43,5 |
42,31 |
- 1,19 |
- 0,42 |
- ( e + i ) the Moon |
|
G - A |
|
223,5 |
224,34 |
0,84 |
|
+ ( e + i ) the Moon |
|
B - D |
|
316 |
316,99 |
0,99 |
|
- ( e + i ) the Moon |
|
A - E |
|
306 |
307,62 |
1,62 |
|
- e (the Sun) |
|
A - F |
308,23 |
309 |
307,62 |
- 1,38 |
- 0,61 |
- e (the Sun) |
|
Middle A-EF |
306,73 |
307,5 |
307,62 |
0,12 |
0,89 |
- e (the Sun) |
|
E - A |
|
126 |
127,39 |
1,39 |
|
+ e (the Sun) |
|
F - A |
128,23 |
129 |
127,39 |
- 1,61 |
- 0,84 |
+ e (the Sun) |
|
Middle EF-A |
126,73 |
127,5 |
127,39 |
- 0,11 |
0,66 |
+ e (the Sun) |
|
C - I |
|
54 |
51,78 |
- 2,22 |
|
- e (the Sun) |
|
C - H |
51,73 |
52,5 |
51,78 |
- 0,72 |
0,05 |
- e (the Sun) |
|
C - G |
|
50 |
51,78 |
1,78 |
|
- e (the Sun) |
|
Middle C-IH |
|
53,25 |
51,78 |
- 1,47 |
|
- e (the Sun) |
|
Middle C-HG |
|
51,25 |
51,78 |
0,53 |
|
- e (the Sun) |
|
G - C |
|
230 |
232,15 |
2,15 |
|
+ e (the Sun) |
|
Suthern entrance |
21,8+0,433=22,23 |
23 |
|
|
0,77 |
|
Inaccuracy of astronomical orientation of the Rondel in Bučany is about the same as it is with the Stonehenge (main stones, thriliths and stones of the Sarse
n's circle). It is necessary to mention that the Stonehenge is dated much later (Stonehenge I 2800-2400 B.C. Stonehenge III 2200-1800 B.C.)See:Hawkins G.S.,White J.B.,1984,p.217-220 , It is also necessary to mention the fact that middle points of western and eastern entrances were considered. Their widths related to the middle points of opposite entrances are 2.5deg.
3.4 Rondel in Bučany as a solar and lunar observatory.
As the computations showed the Rondel in Bučany could have been used as a solar and lu
nar observatory. 9 of total 12 possible extreme values of the ascends and descends of the Sun and Moon are present in the Rondel. The remaining 3 directions are: two for the low Moon, which is possible to observe using the 2 directions which are already present in the Rondel; a direction of the high Moon descend at the summer solstice is not possible to observe because a megaron - a building inside the Rondel disables this. The accuracy of orientation at winter and summer solsices is unique; less accurate is the orientation towards ascending and descending Moon. It is much more difficult to observe the Moon compare to the Sun and so the lower occuracy is acceptable. It is very probable that the Rondel in Bučany served to determine solstices, observations of the Sun and Moon during their times of ascends and descends.4. The Rondel in Bučany as a calendar.
4.1 Suitability of certain directions for neolithic peasants to utilise them as a calendar.
Which of the 12 extreme directions can be appropriate to utilise them as a calendar is in the question. Most of all, seasons change due to the Earth's orbiting the Sun while the axis of rotation of the Earth is inclined to its orbital plane.
Directions towards descends and ascends of the Sun can be used for calendar purposes. Those of the Moon cannot be used, however, as they change in a complex way.
Therefore, only directions that fall between +
e and - e at the ascend and descend of a body are useful for calendar purposes. + e and - e are useful as they determine the time of summer and winter solstices; directions towards high Moon +( e + i ) and also -( e + i ) are not suitable beacuse the Sun never rises and sets in these directions. Directions towards low Moon +( e - i ) and -( e - i ) that besides the solstices can determine another date of the year are useful. These directions determine the following dates in the Rondel: descend of the low Moon at the summer solstice - the Sun sets in this direction on 8 May (7-12 May) and 1 August (30 July - 2 August); ascend of the low Moon at winter solstice - the Sun rises in this direction on 3 November and 6-7 February.These dates could have been used to determine when to finish spring works (8, May) and time to take crops (1, August considering a warmer climate in about 5 degrees). The use of other dates is not clear. 3 November could have served for sowing winter wheat (at present climate the latest term is 15 October). 6-7 February most probably could not be used in connection with agricultural works.
With the above facts in mind we can conclude that the Rondel in Bučany could have been used for calendar purposes as follows: the whole year could have been, according to the agriculturally important dates, divided into 3 periods:
I. From the winter solstice to spring agricultural works 8 May.
II. From spring agricultural works 8 May to taking crops 1 August.
III. From taking crops 1 August to the winter solstice.
Another, less probable scheme of a calendar can be as follows (4 parts):
I. From 6-7 February to spring agricultural works 8 May.
II. From spring works 8 May to taking crops 1 August.
III. From taking crops 1 August to 3 November
IV. From 3 November to 6-7 February.
For shorter periods as those mentioned above the synodic month e.i. changing phases of the Moon could have been used. The synodic month lasts 29 days 12 hours 44 minutes 2.78 seconds (29.5305882 mean days). The synodic month varies due to the eliptical shape of the path of the Moon from 29.25 to 29.83 days. Com
bination of synodic month and solar year is very complex from calendar point of view and so discovery of a lunisolar calendar at time of utilisation of the Rondel in Bučany is not probable.5. Orientation of the Rondel on stars.
Orientation of the Rondel in north-south direction is already given by its orientation towards sunrise and sunset points at winter solsice. The angle formed by points of sunrise and sunset is divided into halves and the resulting direction is that of south. Therefore, a relatively p
recise north-south orientation is present in the Rondel in Bučany. If its orientation on stars is the concern, the northern and southern entrances were examined. A sky and the location of the pole in 3,800 B.C. was analysed. According to the Figure 2. and simulation of the sky using a planetarium projector ZKP-2 made by Carl Zeiss Jena GmbH under the dome with diameter of 10 m which is situated in the Observatory and Planetarium in Hlohovec, the only bright star that rises at the northern entrance at the azimuth of 203deg is Vega of constellation Lyra. The star's magnitude in visual range of spectrum is +0.03. It is the second brightest star in the northern sky.A constellation of the Southern Cross, which was possible to observe that time, descended above the southern entrance (azimuth of 23deg). At present the constellation is not visible in this latitude.
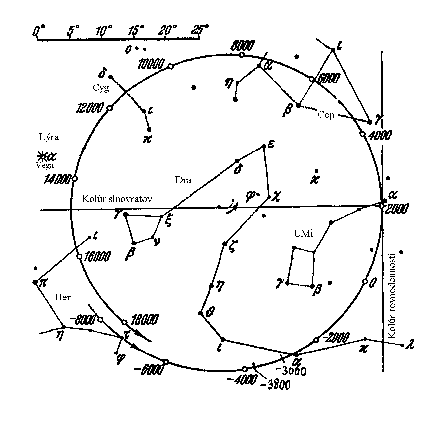
Figure 2. The location of the pole among the stars changes due to the precession. Depicted is the location of the pole in 3,800 B.C.
Low at the horizon only bright stars can be observed because the absorption of the light by the atmosphere is high. With clear sky by unaided eye the stars up to the 6th magnitude can be seen; with cloudy or dusty conditions it decreases to the 4th magnitude. The influence of absorption of light by atmosphere at the horizon can be seen in the table below, Allen C.W.,1977,p.182-185
|
h (deg) |
Absorption (magn.) |
Magnitude of Vega |
visibility |
|
0o |
6,4 |
6,43 |
No |
|
0o 35' |
5,4 |
5,43 |
Very poor |
|
1o 42' |
3,96 |
3,99 |
Poor |
|
2o 46' |
3,07 |
3,10 |
Poor |
|
3o 48' |
2,49 |
2,52 |
Relatively good |
|
4o 50' |
2,08 |
2,11 |
Good |
|
5o 52' |
1,78 |
1,81 |
Good |
|
6o 53' |
1,55 |
1,58 |
Good |
|
7o 53' |
1,38 |
1,41 |
Very good |
An increase of 1 in magnitude means that the intensity of lightbeam decreases 2.512 times. 8 degrees above horizon Vega gets 3.56 times fainter; 5 degrees above horizon it is even 6.79 times fainter than it normally appears. In 3,800 B.C. Vega was a circumpolar star, e.i. it did not set during the 24 hour rotation.
However, in the real sky it was practically invisible at the horizon and only appeared from 5-8 degrees above the horizon, so that to an observer it seemed that it ascended at that point.
Figure 3. Constellation of Lyra with its brightest star Vega by Tirion W., 1981
In Rondel in Bučany it was possible to locate Vega 5-8 degrees above the horizon at the azimuth of 203 degrees. It did not dep
end on the real horizon which is almost 0 degrees as right above the horizon the star was not visible.6. Conclusion and Discussion.
The Rondel in Bučany is oriented in 9 of 12 extreme astronomical directions. Accuracy of this orientation practically elimi
nates possibility of an accident. All the astronomical directions are fairly observable as far an observer with the height of 1.6 m and the height of palisade at the point of an important direction of 1.5 m is considered. If estimated heights of palisades 1.6 – 3.6 m (Weber Z.,1969) are considered then it was not possible to use the direction of setting sun at winter solstice and directions to the high Moon after finishing the building. However, while building the Rondel, at first all the directions to winter and summer solstices had to be erected. Otherwise it would not have been possible to point all the entrances towards the low Moon and to use the Rondel for calendar purposes as well. Because the directions to the low Moon are present, with a period of 18.61 in which the same position of objects occurs, the process of building the Rondel would have taken at least 19 to 38 years.It was only possible to use the Rondel to observe very bright stars like Vega, which with excetion of Vega itself were not located at the northern entrance (because of the precession). Towards the southern entrance is only located bright star Acrux of constellation Southern Cross with magnitude +0.9 and Rigil Kent of constellation Centaurus with magnitude –0.27.
The purpose for observing these stars is not clear if we do not consider cult events.
The Rondel as a building was built in a very useful and fashion way without any revisions to the directions which shows that it was probably built according to an older scheme.
7. Special thanks.
In the end I would like to thank PhDr. Gertrúda Březinová, CSc. from the Archeological Dept. of SAV in Nitra for her kind help with archeology literature and for revisions of the presented paper from archeological point of view.
References:
Allen C.
W.,1977 Astrofizičeskije veličiny, Mir, Moskva 1977Astronomičeskij Ježegodnik 1979 , Nauka, Leningrad 1976, s.638-639
Astronomičeskij Ježegodnik 1979a, Nauka, Leningrad 1976, s 660-663
Astronomičeskij kalendar,postajannaja časť 1981,s.590 Nauka, Moskva,
1981Berliner Astronomisches Jahrbuch 1959, Akademie Verlag , Berlin 1957,s.424-425
Bucha V.,1975 Geomagnetické pole a jeho přínos k objasnění vývoje Země., Akademia, Praha 1975
Bujna J., Romsauer P.,1982. Záverečná výskumná sezóna v Bučanoch. In:Archeolo
gické výskumy a nálezy na Slovensku v roku 1981 , Nitra 1982 s.59-64Bujna J.,Romsauer P.,1986 Siedlung und Kreisanlage Der Lengyel-kultur in Bučany. Internationales Symposium uber die Lengyel-Kultur, NovéVozokany 5-9.11.1984, Nitra-Wien 1986
Bujna J.,Rom
sauer P.1987.Osada neolitických roľníkov v Bučanoch. Krásy Slovenska , LXIV,6/87,10-12Duncan J.Ch.,1946 Astronomy,Harper & Brothers Publishers,New York-London 1946,p.82-83
Hawkins G.S.,1977 Krome Stounhendža Mir, Moskva, 1977, s.248
Hawkins G.S.,White J.B
.,1984 Razgadka tajny Stounhendža, Mir, Moskva 1984Horský Z., 1986 Vorläufige Untersuchungen ůber vermutliche astronomische Orientierung einiger neolithische Kreisgrabenanlagen, Internationales Symposium uber die Lengyel-Kultur, Nové Vozokany 5-9.11.1984
, Nitra-Wien 1986, 83-87Chalchunov V.Z. Sferičeskaja astronomija,, Nedra, Moskva 1972, s.66-68
Podborský V.,1983 Die Kreisgrabenanlage zu Těšetice und moglichen mährischen Parallelen, Mitteilungen der osterreichischen Arbeits Gemeinschaft fur Ur-und Fruhg
eschichte XXXIII.,in pressTirion W.,1981 Sky Atlas 2000,0 Cambridge, USA, Masssachusets, 1981, 26 máp
Weber Z., 1985 Astronomická orientace rondelu Z Těšetic -Kyjovic, okr.Znojmo. Sborník prací Filozofické fakulty Brnenské
univerzity. Studia Minora facultatis philosophicae Universitatis Brunensis E30, 1985, 23-39Weber Z.,1969 O třetím rozměru v archeologii, Sborník prací filosofické fakulty Brnenské University E 14, 1969, 219-222
Wood E.J.,1978 Sun,Moon and Standing Stones,Oxford University Press, Oxford,London, New York 1978
Wood E.J.,1981 Solnce, Luna i drevnije Kamni, Mir, Moskva 1981, s.83-105